강의자료 공부
01. DP(1)
1) Divide and Conquer(분할정복) vs DP
- 분할정복: 서로 겹치지 않는 분리된 서브 문제로 나누고, 각각을 재귀적으로 해결한 후 결합하여 원래 큰 문제 해결함
- DP: 중복된 서브 문제를 푸는 경우, 이미 해결된 서브 문제는 메모해두어서 재활용함(예: 피보나치 수열 → 일반적으로 나이브하게 코딩하면 큰 수 계산 오래 걸림)
- DP는 일반적으로 최적화 문제에 활용됨
💡 특성: Optimal substructure(최적 부분 구조 / DC, DP 둘 다 가짐) + overlapping(DP만 가짐)
2) DP 단계
- optimal solution의 구조를 특성화 시킴
- optimal soultion의 값을 재귀적으로 정의함
- optimal soultion의 값을 bottom-up 방식으로 계산함 (optimal value 구하기)
- 계산된 정보를 통해 optimal solution을 구성함
3) Rod-Cutting problem(막대 자르기 문제)
- 가장 수익 높게 막대를 자르는 문제
-재귀식
- 길이가 n인 막대의 최대 수익 rn은 더 짧은 막대의 최적 수익을 기반으로 표현 가능


- 크기 n인 원래 문제를 풀기 위해 더 작은 크기의 같은 유형 문제들을 해결함
- 막대 자르기 문제는 optimal substructure을 보임: 즉, 하나의 문제의 optimal solution은 독립적으로 해결할 수 있는 관련 subproblem의 optimal solution을 포함하고 있음
- 그냥 naive하게 재귀식으로 풀면
- 2^n개의 node (호출 횟수)
- 2^(n-1) leaves (막대 자르는 경우의 수=solution개수)
- overlapping subproblem들을 기억하며 풀자 → DP
- time-memory trade-off임(시간 또는 메모리를 반비례 관계로 쓰는데, DP는 시간을 줄이는 대신 메모리를 많이 씀)
- Bottom up이나 memoization 사용하면 2^(n-1) → Θ(n^2) 로 줄일 수 있음
-Memoization vs Tabulation
- Memoization: Top-down방식 → 재귀 호출을 통해 문제를 풀면서 결과 저장한 후 재활용, 필요할 때마다 계산됨
- Tabulation: Bottom-up 방식 → 작은 문제부터 순서대로 계산해서 재활용, 모든 값을 미리 계산해서 테이블에 저장하고 이를 통해 더 큰 문제를 해결함
⇒ 여기선 tabulation, bottom up 방식 사용
02. DP(2)
- 각 문제 재귀식 제시 → 테이블 채우기
1) Matrix-Chain Multiplication (연쇄 행렬 곱셈)
- n개의 행렬이 있을 때, 이것들을 곱하는 순서에 따라 곱셈 횟수가 크게 달라짐 → 제일 적은 곱셈 횟수를 가지는 순서를 찾자
- 과정
- 구조 특성화: 행렬 곱셈의 특정 구간 Ai ~ Aj를 계산할 때 잘라서 Ai~Ak + Ak+1~Aj로 분할하여 계산한 결과를 사용함
- 재귀식 정의: 따라서 Ai~Ak를 계산하는 비용, Ak+1~Aj를 계산하는 비용, 두 결과 행렬을 곱하는 비용으로 재귀식 정의 가능
-재귀식
- 최소 비용을 저장하는 테이블 m[i][j]에서 k를 기준으로 분할
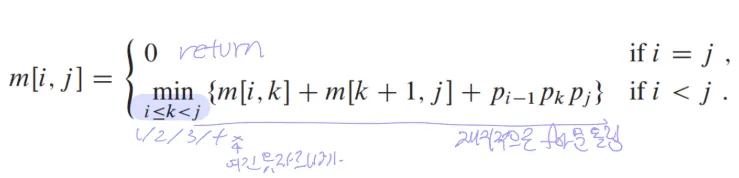
3. bottom-up 방식으로 계산: 행렬 곱셈 구간 길이 L을 2부터 n까지 늘려가며 m[i][j]계산함

- 완전 탐색을 하면 지수시간 걸림 → DP로 하면 O(n^3)시간에 Θ(n^2) 공간(2차원 배열)
2) Maximum-Subarray (최대(연속)부분 합)
- 존 분할 정복 문제를 DP로도 빠르게 풀 수 있음
03. DP(3)
- 각 문제 재귀식 제시 → 테이블 채우기
1) Longest Common Subsequence (LCS)
[DP] LCS (Longest Common Subsequence)
LCS ( Longest Common Subsequence )두 문자열을 입력 받고, 그 중에서 최장 공통 부분 수열을 찾는 문제이다. -원리두 문자열 X(x1, x2, x3...), Y(y1, y2, y3...)가 있을 때 가장 마지막 원소부터 비교해본다.같은
rim08.tistory.com
- 브루트 포스로 하면 지수 시간이 걸림 → DP로는 두 문자열 길이에 따라 결정
- optimal value time complexity: Θ(n*m) //행렬 크기
- optimal solution time complexity: Θ(n+m) //화살표 따라 이동하는 최대 길이
- 과정
- 0행 0열은 다 0으로 초기화
- 그 안쪽부터 순서대로 계산, 문자가 같다면 왼쪽 대각선에 가져오고 1더함
- 문자가 다르다면 왼쪽과 위쪽 중 큰 값을 그대로 가져옴
- 이때 값은 optimal value로 LCS 길이 구한 거고(마지막 행과 열의 값) / 화살표 순서대로 따라가면 optimal solution임(왼쪽 대각선인 경우만 따라가서 거꾸로 출력)
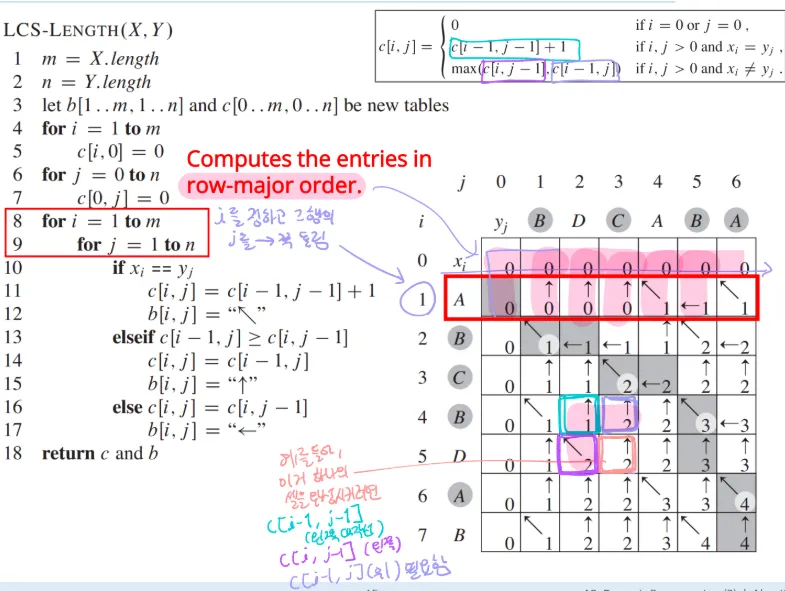
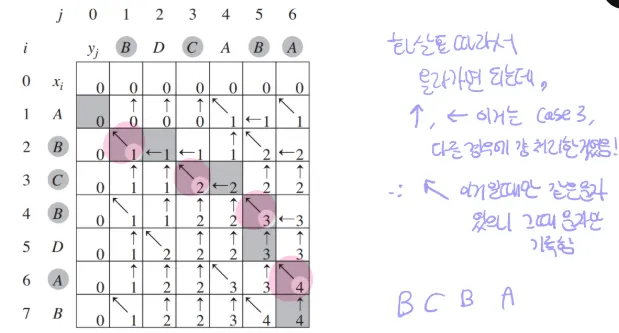
- 화살표 저장 b테이블 없이 값 저장하는 c테이블 만으로도 가능함(왼쪽이랑 위 비교해서 최댓값인쪽으로 가면 되니까)
- 이 방법이 space complexity를 별로 줄이지는 못하지만 조금 최적화는 가능함
- LCS 길이(optimal value)만 구하고 싶으면 space 줄일 수 있음 → 계산하는 행과 열 두 줄만 필요하고 이미 계산 된 나머지 위, 왼쪽은 날려버리면 됨(맨 마지막만 정답이니까)
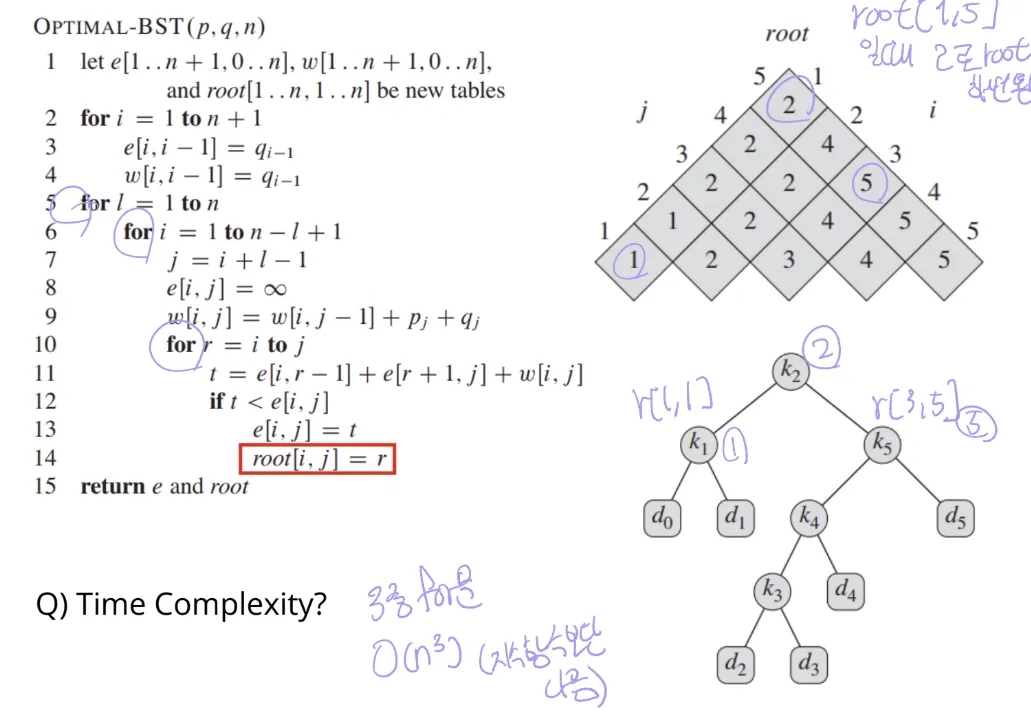
2) Optimal Binary Search Tree (OBST)
-정의
- 최적 이진 탐색 트리
- optimal binary search tree: 검색 확률에 따라 구성하여 평균 검색 비용(가중평균)을 최소화 시킴(자주 나오는 것들을 위쪽으로)
- 입력: n개의 key / 각 key가 검색될 확률 p / key 아래에 존재할 가능성이 있는 더미 키 d / 더미 키로 빠질 확률 q
-OBST가 필요한 이유
- 기존 binary search tree: 왼쪽은 작고 오른쪽은 큰 값으로 노드 구성 → 사전을 만든다고 했을 때, 자주 나오는 단어가 아래쪽에 있는 경우 검색 횟수 많이 필요함
- → 검색 빈도가 높은 키를 루트 쪽에 배치하여 검색 시간을 줄이기 위해 OBST 사용 → 평균 검색 비용 최소화 시킬 수 있음
-DP 과정
- 구조 특성화: 트리 전체가 optimal 하다면 왼쪽 서브 트리와 오른쪽 서브 트리도 optimal해야 됨(만약 서브 트리가 optimal이 아니라면 전체도 개선 가능성이 있다는 뜻인데 그럼 모순됨)
- 재귀식 정의
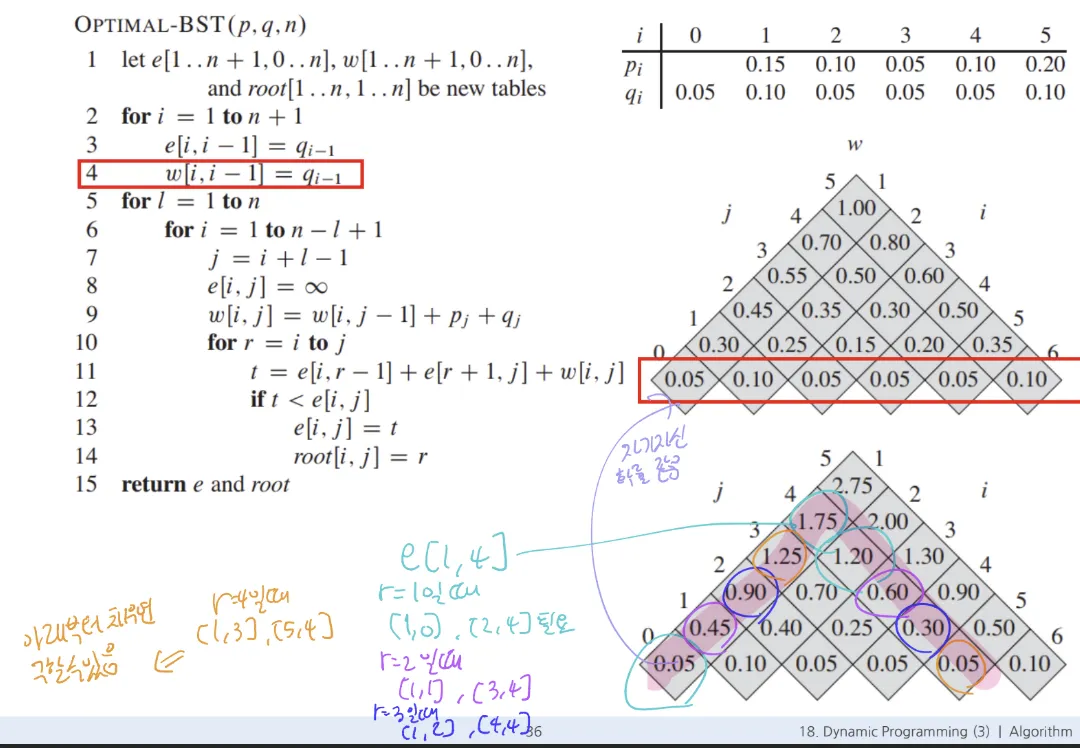
- expected cost = e[i, j] //key인 ki~kj로 이루어진 OBST의 검색 비용, i부터 j까지 root로 세워서 테스트 해 봄

- e[i, i-1]: qi-1 //더미 키 하나만 있을 때는 자기 자신의 확률임, e[3,2]인 경우 q2임

- 재귀식:


- expected cost = e[i, j] //key인 ki~kj로 이루어진 OBST의 검색 비용, i부터 j까지 root로 세워서 테스트 해 봄
- DP 계산

'🌙CS > 알고리즘' 카테고리의 다른 글
| Greedy (0) | 2025.01.07 |
|---|---|
| Backtracking (1) | 2025.01.07 |
| MoM (2) | 2025.01.07 |
| [Backtracking] 미로 탈출 (0) | 2024.11.22 |
| [DP] LCS (Longest Common Subsequence) (2) | 2024.11.21 |
