강의자료 공부
01. Greedy(1)
1) Greedy Algorithm 개념
- 현재 순간에서 최적의 선택을 하는 방식으로 문제 해결함 → 이를 반복하여 전체적으로도 최적의 해답에 도달하려고 함
- 항상 optimal solution을 보장하진 않지만 많은 문제에서는 optimal solution 찾을 수 있음
- 특성
- Optimal Substructure(DP도 가짐): 부분 문제의 최적 해가 전체 문제의 최적 해를 구성함
- Greedy Choice Property: 매 단계에서의 최적 선택이 전체적으로도 최적의 해로 이어질 수 있음
2) Activity Selection 문제
- 여러 활동이 하나의 자원을 공유해야 될 때, 서로 활동들이 겹치지 않으면서 최대한 많은 활동을 선택하는 문제 (ex: 강의실 하나인데 강의가 여러개일 때 타임테이블 구성)
- 각 활동 ai는 시작 시간 si, 종료시간 fi로 구성 → [si, fi)
- 끝은 열린 구간이기 때문에 다음 활동 시작이랑 겹쳐도 ㄱㅊ
- 활동들은 종료 시간 기준으로 정렬되어 있음을 가정

-DP 대신 Greedy 쓰는 이유
- DP로 접근은 가능 → DP로 하면 아래 재귀식처럼 됨

- 가능한 모든 k를 다 탐색해야 하므로 시간이 오래 걸림 → Greedy하게 하자
- Greedy로 끝나는 시간이 빠른 활동들을 선택하면 더 많이 선택 가능해짐
-Greedy 과정
- 활동들을 종료시간 기준으로 정렬
- 가장 빨리 종료하는 활동 선택
- 선택된 활동과 겹치지 않는 다음 활동을 반복적으로 선택
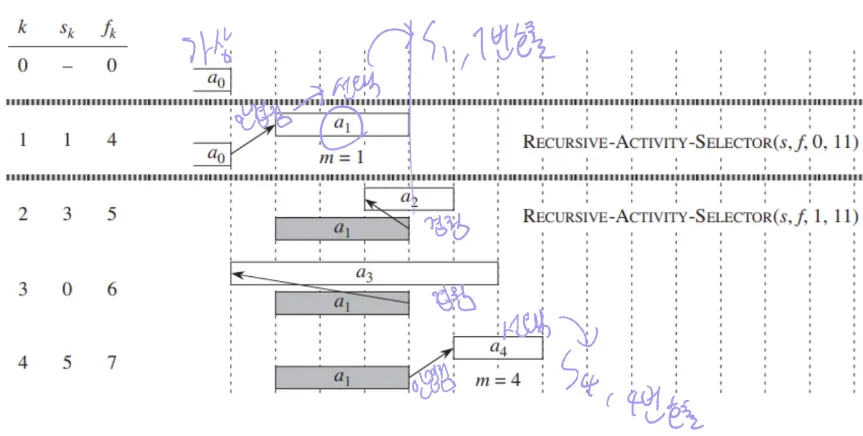
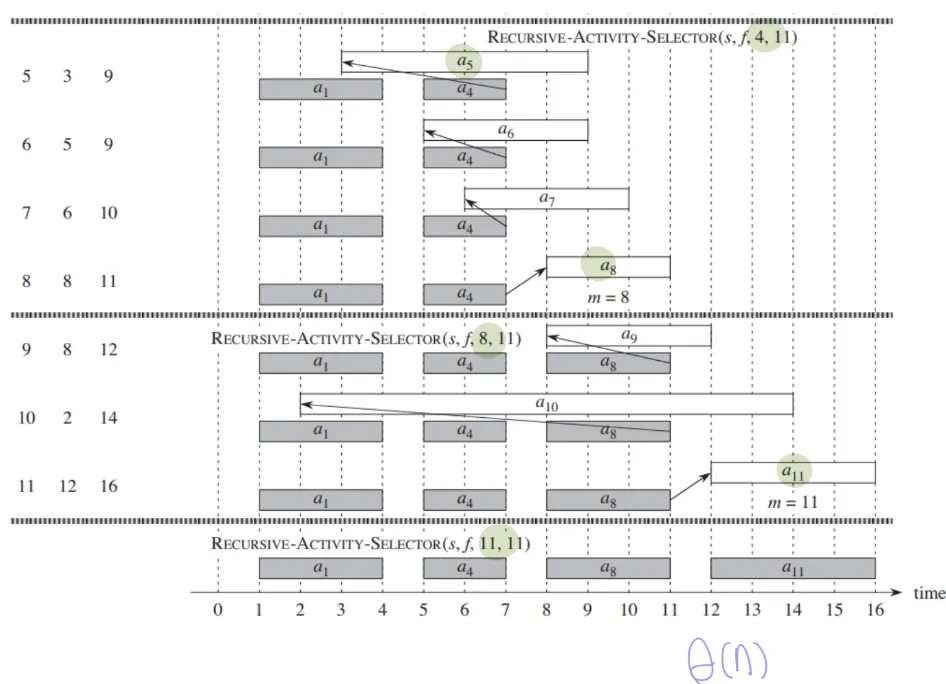
⇒ 시간 복잡도: Θ(n) / 정렬 포함 시 O(n lg n)
3) Greedy Stays Ahead 증명
- Greedy 선택이 정말로 optimal solution을 제공하는지?
- → <Greedy Stays Ahead>(: 그리디가 선택한 해가 최적 해보다 앞서거나 같음)로 증명할 수 있음
- Notation
- O: Optimal solution
- g_sol: greedy solution
- |O| = |g_sol|, 크기가 같음을 보이는 것만으로도 충분함
- 각 단계에서의 g_sol의 선택이 O 선택보다 늦지 않음을 증명하기
- 보조 정리1: 가장 빨리 종료하는 활동을 선택했기 때문에 첫번째 차례에선 무조건 g가 더 빨리 끝나거나 똑같음
- 그럼 귀납적으로 그 다음 단계도 g≤O가 됨

- g가 k개의 활동 선택, O가 k+1개의 활동을 선택한다고 가정하면 (O가 더 좋다는 뜻)
- g가 Ok+1을 선택하지 않은 상황은 그리디 절차와 모순됨
- 따라서 g와 O의 크기는 같으며 g는 최적해가 됨
⇒ 귀납법과 귀류법을 통해 g(sol)의 선택이 항상 O의 선택과 일치하거나 효율적임을 증명함 → 이를 통해 그리디 알고리즘이 항상 최적의 해를 제공함을 증명할 수 있음
01. Greedy(2)
1) Minimize Maximum Lateness
- 최대 지연 시간 최소화: 일정한 시간 내에서 여러 요청이 주어질 때, 각 요청의 lateness를 최소화하는 스케줄을 찾는 문제 (ex: 3전공의 과제들 중 뭐 먼저 할 건지)
- request ri는 deadline di를 가짐, 그걸 수행하는데 걸리는 시간은 ti임
- 따라서 fi = si + ti로 완료 시각 f를 계산할 수 있음 → 이 fi가 di보다 작아야 되는데, 만약 마감 시각을 넘어선다면 그만큼 lateness가 발생함
- 상황은 2가지
- 제때 끝나거나 → li = 0
- 기간 넘기거나 → fi - di

- 따라서 합계엔 관심 x, 각각이 작아야 됨

-Potential Option
- SPTF: 프로세싱 타임이 짧은 것부터 먼저 → optimal 보다 더 안 좋아질 수 있음
- Minimum Slack Time First: slack time(여유 시간)이 짧은 것부터 → 마찬가지로 좋진x

3. EDF: dead line이 빠른 것부터 먼저 → optimal solution 가능
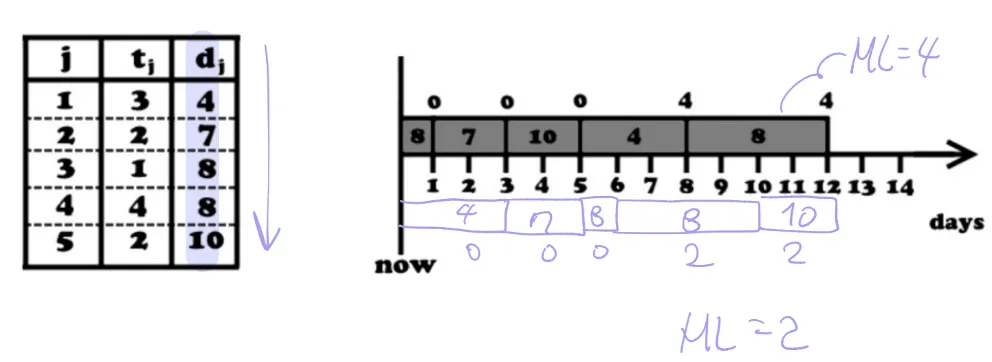
⇒ 시간 복잡도: 정렬 필요시 Θ(nlgn), 정렬되서 들어오면 Θ(n)
2) Exchange Arguments
- EDF 방식인 그리디 스케줄이 왜 optimal한지 증명하기 위해 <exchange arguments> 방식으로 증명함
- optimal solution을 최적성을 해치지 않는 선에서 변화시키다 보면 그리디 스케줄과 동일해 짐 → 그럼 그리디고 optimal이라는 원리
- 이 증명법은 다음 2가지를 보임
- optimal solution에서 greedy 스케줄로 변환 가능하다.
- 변환 과정에서 optimal solution의 cost(lateness)는 변하지 않는다.
- key facts
- Removing gaps can only improve. (쉬는 시간, 비어있는 간격을 없애는 것은 무조건 좋아짐)
- A gapless schedule with any inversion has a back-to-back inversion (간격이 없는 스케줄에서의 역전 관계는 인접(백투백) 역전 관계를 포함함)
- Swapping back-to-back inversions can only improve (인접 역전 관계를 교환하면 무조건 좋아짐)
- Swapping back-to-back inversion decreases the number of inversion (인접 역전 관계를 교환하면 역전 관계의 총 개수가 감소됨)
- Swapping back-to-back requests with the same deadline doesn’t matter (동일 마감 기한을 가진 요청 간의 교환은 결과에 영향 미치지 않음)
- fact 5가지를 이용하여 증명하는 과정
- 갭 제거(최적성 해치지 않음)
- 역전 관계 해결: 인접 역전 관계를 교환하여 점차적으로 모든 역전 관계 제거함(최적성 해치지 않음)
- 동일 마감 기한을 가진 요청들을 그리디대로 정렬함 (최적성 해치지 않음)
- 모든 과정이 완료되면 optimal solution은 greedy가 생성한 스케줄과 동일해짐
- 따라서 그리디 알고리즘은 optimal solution을 제공한다고 할 수 있음
01. Greedy(3)
1) Huffman codes (=Prefix codes)
- 데이터 압축 알고리즘으로, 빈도가 높은 문자는 짧은 코드로, 낮은 문자는 긴 코드로 표현하여 파일의 크기를 줄이는 방법
- Fixed-length code는 간단하지만 variable-length code로 허프만 코드를 사용했을 때 약 25%의 용량을 절약할 수 있음
-Prefix (free) codes
- 어떤 codeword도 다른 codeword의 prefix(접두사)가 아님
- 즉 a가 0이면, 0으로 시작하는 문자는 없음, b가 101이면 101로 시작하는 문자 없음 → unambiguous(모호성이 생기지 않음)
- 어떤 문자라도 항상 optimal data로 압축시킬 수 있음
- decode한 걸 그대로 합치면 encode하는 것임(a:0, b:101, c:100으로 decode한 걸 encode하면 0101100임)
2) Decoding Tree
- 허프만 코드의 optimal code는 항상 full binary tree로 표현됨
- 모든 non-leaf node는 자식 node 2개 가짐
- 트리의 leaf node는 각 문자를 나타냄

- 알파벳이 C개 있으면 internal node(non-leaf node)는 C-1개임

- B(T): 트리 하나의 cost = encode file의 필요한 bit 수
- c.freq: 문자 마다의 빈도 수
- dt(C): T트리의 C의 depth = 문자 C에 대한 codeword의 길이
⇒ B(T)가 작을 수록 트리 비용이 낮아지는 것이고, 가장 낮아진 것이 optimal 한 것임
-Constructing a Huffman Code
- optimal prefix code를 구성하는 그리디 알고리즘 = 허프만 코드
→ 즉, greedy choices를 통해 디코딩 트리 구성할 수 있음
- 과정
- 빈도수대로 정렬
- 가장 빈도수 적은 두 노드를 묶음 → 하나의 internal node (key는 더한 값)로 다시 정렬됨
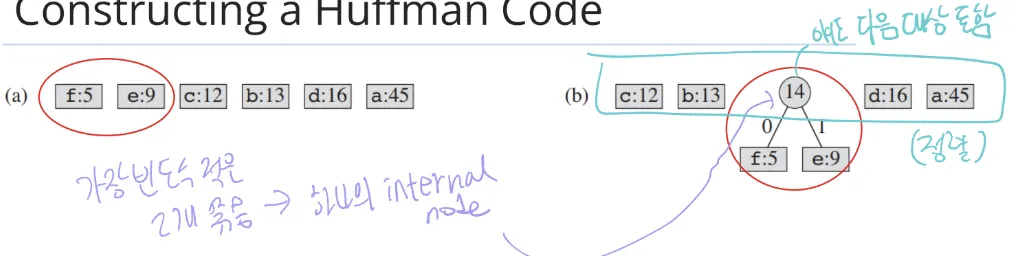

3. 이진 트리를 따라가며 왼쪽은 0, 오른쪽은 1로 표시하면 디코딩 한 거임
⇒ 시간 복잡도: O(nlgn) //Min heap 생성, 노드 삽입 및 삭제가 저 시간으로 걸림
3) Correctness of Huffman’s Algorithm
- 2가지 속성 가짐
i) Greedy Choice Property
- 보조 정리: 등장 빈도가 가장 낮은 두 문자는 항상 동일한 깊이 가지며, 마지막 비트만 다르게 코딩됨 → leaf node이자 형제 노드로 각각 0, 1로 디코딩
- 이는 그리디가 항상 최적 트리를 생성함을 보장함
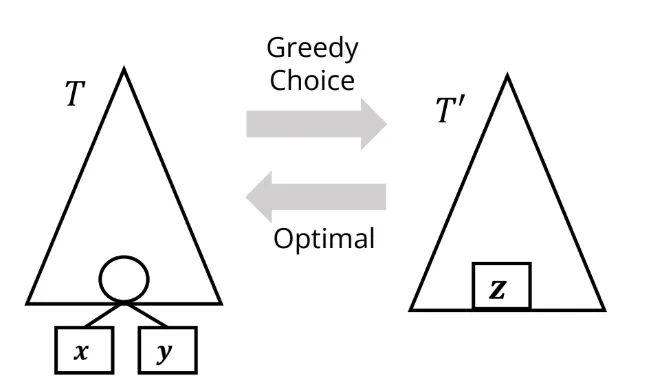
ii) Optimal Substructure Property
- 병합 문자 z가 optimal이면 전체 문제인 x, y 포함된 트리도 optimal이 됨 → 즉 작은 트리가 opt면 큰 트리도 opt가 된다는 논리임

'🌙CS > 알고리즘' 카테고리의 다른 글
| DP (2) | 2025.01.07 |
|---|---|
| Backtracking (1) | 2025.01.07 |
| MoM (2) | 2025.01.07 |
| [Backtracking] 미로 탈출 (0) | 2024.11.22 |
| [DP] LCS (Longest Common Subsequence) (2) | 2024.11.21 |
