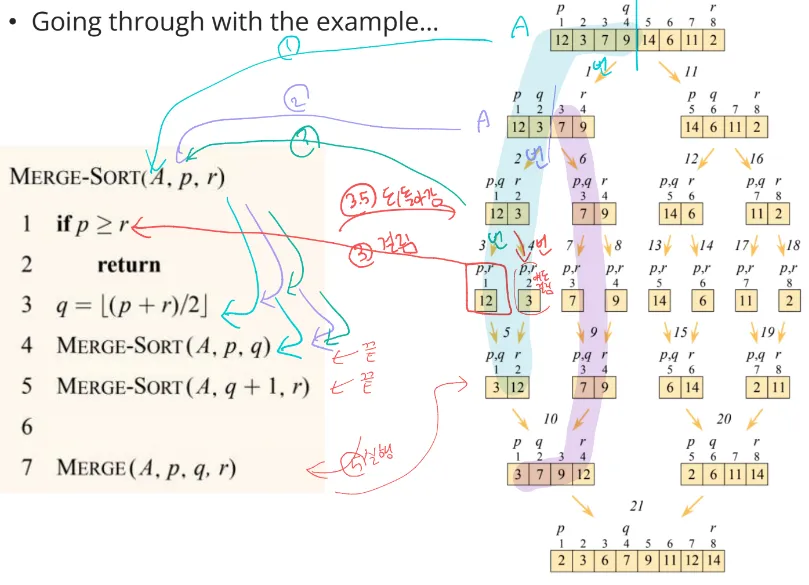
01. Merge sort
- 병합 정렬은 분할 정복(Divide-and-Conquer) 방식을 사용함
- Divide(분할): 문제를 여러 개의 더 작은 문제로 나누는 과정
- 병합 정렬: 원래 크기 n의 배열을 정확히 절반, n/2으로 나누어 두 개의 하위 배열로 나눔(실제 메모리 상에서 분리하는 건 x, 그냥 경계선을 index로 정하는 거임)
- Conquer(정복): 분할된 하위 문제들을 재귀적으로 해결하는 과정으로, 하위 배열들이 더 이상 분할할 수 없을 만큼 작아질 때(예: 배열의 크기가 1일 때)는 간단하게 풀어서 처리함
- 병합 정렬: 2개의 하위 배열을 재귀적으로 정렬하다가 1개의 원소만 남을 때 간단히 처리 (straightforward solution(종료조건): p ≥ r일 때 return;)
- Combine(결합): 정렬된 두 하위 배열을 하나의 배열로 병합하는 과정
- 병합 정렬: 각 배열이 이미 정렬되어 있기 때문에, 각 배열에서 차례대로 작은 원소를 선택하여 최종 배열에 결합시키면 됨
- Divide(분할): 문제를 여러 개의 더 작은 문제로 나누는 과정
02. Analysis of Merge sort
- merge sort의 divide-and-conquer 알고리즘은 ‘Recurrence equation(재귀식, 점화식)’으로 분석할 수 있음
- 점화식

- Merge sort의 점화식

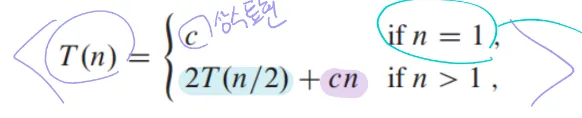
- 점화식 계산
- Recursion Tree(재귀 트리)

'🌙CS > 알고리즘' 카테고리의 다른 글
| Sorting in Linear Time (2) | 2024.10.26 |
|---|---|
| Heap Sort (2) | 2024.10.26 |
| Matrix Multiplication (Strassen’s Algorithm) (1) | 2024.10.26 |
| The Maximum-Subarray Problem (1) | 2024.10.26 |
| Analyzing Algorithms (0) | 2024.10.26 |
