01. Matrix Multiplication by Divide-and-Conquer
- 행렬 곱 연산시, 3중 for문 사용 -> Θ(n^3)
- 분할정복으로 계산: 4개씩 정사각형으로 나누어서 연산하고 합치는 과정


- 각 재귀식 라인마다 T(n/2) size임 -> 8줄이니 8T(n/2)가 됨
- 더하는 과정: (n/2) x (n/2) = (n^2/4)만큼의 덧셈이 필요함 ⇒ Θ(n^2)
- total time
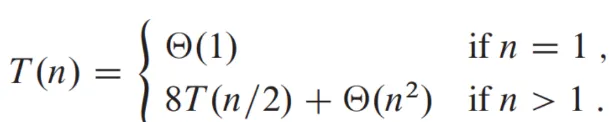
-> Master Method로 풀면 Θ(n^3) -> 분할정복을 해도 행렬 곱은 똑같이 Θ(n^3)으로 나오는게 핵심
02. Strassen’s Method
- a값을 줄이는 걸 목표로 함 → 8T()는 큰 문제가 8개로 나눠진다는 뜻이니 그걸 7로 줄이자(곱셈 줄이는 대신 덧셈 조금 늘어나긴 함)
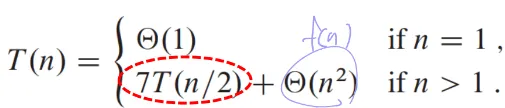
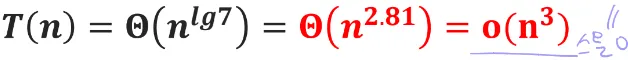
'🌙CS > 알고리즘' 카테고리의 다른 글
| Sorting in Linear Time (0) | 2024.10.26 |
|---|---|
| Heap Sort (0) | 2024.10.26 |
| The Maximum-Subarray Problem (0) | 2024.10.26 |
| Designing Algorithms (0) | 2024.10.26 |
| Analyzing Algorithms (0) | 2024.10.26 |
