01. Heap
- Heap은 배열을 기반으로 하는 complete binary tree(완전이진트리: 마지막층 빼고 다 채워짐, 마지막 층은 왼쪽부터 채워진 상태)
- Max-Heap: 부모 노드 ≥ 자식 노드
- Min-Heap: 부모 노드 ≤ 자식 노드
- index 구하기
- Parent: [자식노드/2](내림)
- left child: 2*i
- right child: 2*i + 1
- 높이: 힙의 높이는 루트에서부터 리프 노드까지의 가장 긴 경로의 간선 수로 정의됨
- node의 높이: 가장 긴 자식 경로
- heap의 높이: root의 높이
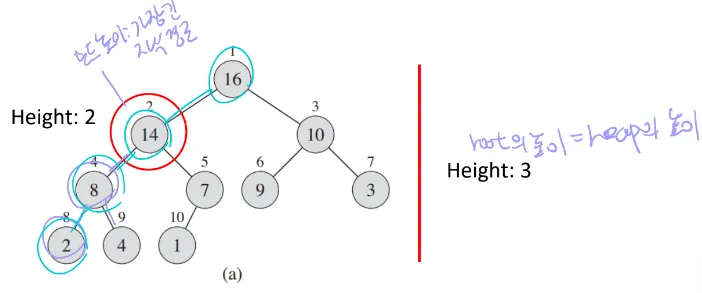
★ 높이가 h인 힙: 최소 2^h개의 노드(맨 아래 왼쪽 노드 하나 달림) / 최대 2^(h+1) -1 개의 노드(포화 이진 트리)

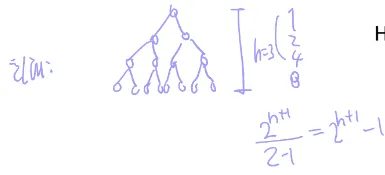
☆n개의 요소를 가진 힙의 높이는 [log n](내림)에 비례함

02. Max-Heapify
- Max-Heapify는 배열에서 부모 노드 < 자식 노드일 때, 부모 노드를 아래로 내려 자식들 중 큰 값과 교체하여 Max-Heap 성질을 유지하는 과정임
- 이를 통해 루트에서 시작한 Max-Heap의 불균형을 해결할 수 있음
★ 호출되는 노드의 아래 노드들은 max heap조건 만족하고 있어야 됨!!
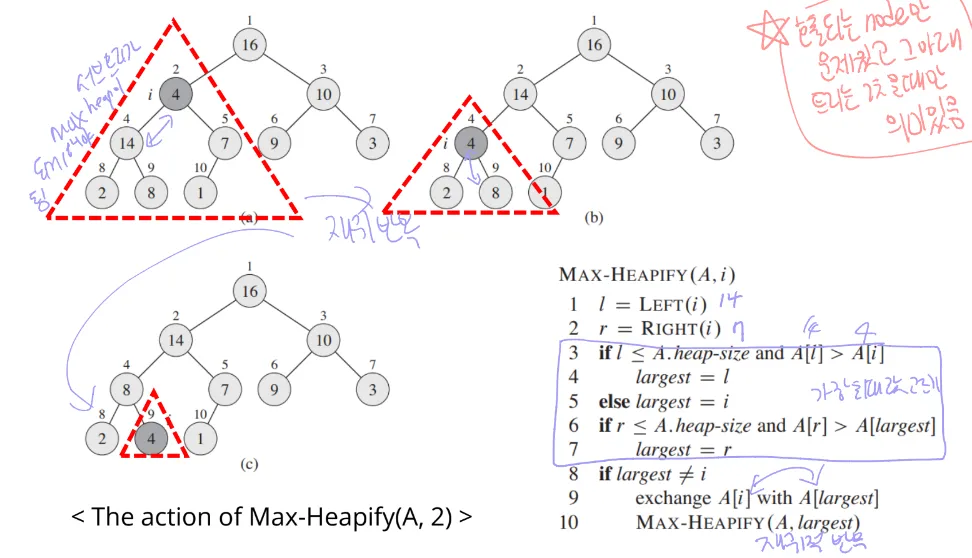
Max-Heapify 점화식

- Master Method: a=1, b=3/2(반대임)
- w, f 둘 다 1로 case 2
- w*log n = T(n) = Θ(log n)
- T(2n/3) size인 이유
- Max-Heapify에서 재귀적으로 호출될 때, 완전 이진 트리이기 때문에 보통 왼쪽 서브트리가 더 클 가능이 높음

03. Heap sort
- Heap Sort는 Max-Heap을 이용한 정렬 알고리즘 (내림차순: max heap / 오름차순: min heap)
- 배열을 힙으로 만든 후, 루트 값을 배열의 끝으로 보내고 나머지 요소들에 대해 Max-Heapify를 반복하여 정렬을 완료함 (맨 마지막은 의미x, 그의 부모부터 기준으로 삼고 max-heapify로 정렬, 아래부터 시작해서 위로 올라오는 과정임 = 대상의 아래 트리는 다 정렬된 상태가 됨)
- 랜덤으로 주어진 배열을 max-heap으로 build - > O(n)
- 힙에서 최대값(루트)를 추출하여 배열의 끝에 배치함 → 남은 트리에 대해 max-heapify 반복 → O(lg n)
- 계속해서 루트의 최대값을 추출하여 배열에 끝에 넣는 걸 반복하면, 최종 배열은 작은 값부터 순서대로 정렬됨(트리도)
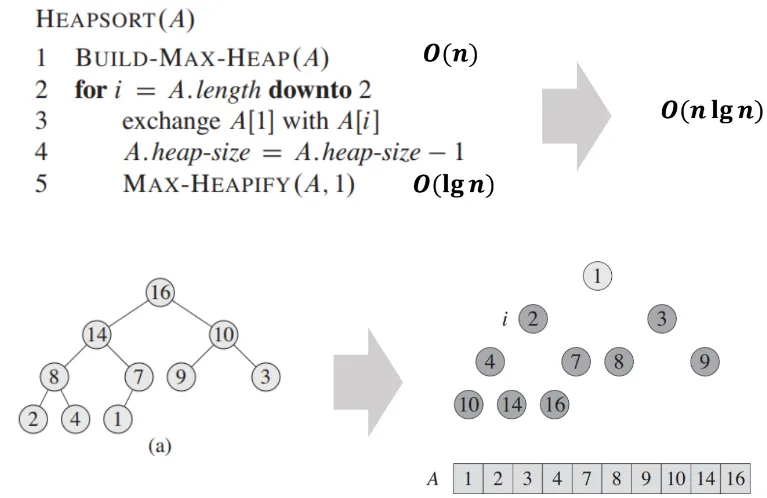
04. In-place & Stable sorts
1) In-place (제자리 정렬)
- 추가적인 메모리 공간 없이, 주어진 입력을 변환하는 알고리즘
- 작은 상수 공간은 무시할 수 있어서 그정도는 inplace하다고 봄
| Inplace sorting | Not In-place sorting |
| Insertion sort | Merge sort |
| Heap sort | Counting sort |
| Quick sort | Radix sort |
| Selection sort | Bucket sort |
| Bubble sort | |
| Shell sort |
2) Stable (안정 정렬)
- 동일한 값을 가지는 요소들이 입력 순서대로 출력되는 정렬 알고리즘
| Stable sorting | Unstable sorting |
| Insertion sort | Heap sort |
| Merge sort | Quick sort |
| Bubble sort | Selection sort |
| Counting sort | Shell sort |
'🌙CS > 알고리즘' 카테고리의 다른 글
| Medians and Order Statistics (0) | 2024.10.26 |
|---|---|
| Sorting in Linear Time (2) | 2024.10.26 |
| Matrix Multiplication (Strassen’s Algorithm) (1) | 2024.10.26 |
| The Maximum-Subarray Problem (1) | 2024.10.26 |
| Designing Algorithms (1) | 2024.10.26 |
