01. Quick Select
- Quick Select는 선택 문제(특정 순서 통계값을 찾는 문제)를 해결하는 분할 정복 알고리즘
- 주어진 배열에서 i번째 작은 값을 찾는 문제를 퀵 정렬(Quick Sort)의 개념을 변형하여 해결함
- 퀵 정렬처럼 피벗(pivot)을 사용해 배열을 두 부분으로 나누고, 그 중 하나의 부분만을 선택해서 재귀적으로 진행함
- Quick Select의 시간 복잡도는 최악의 경우 O(n^2)이지만, 평균적으로는 O(n)
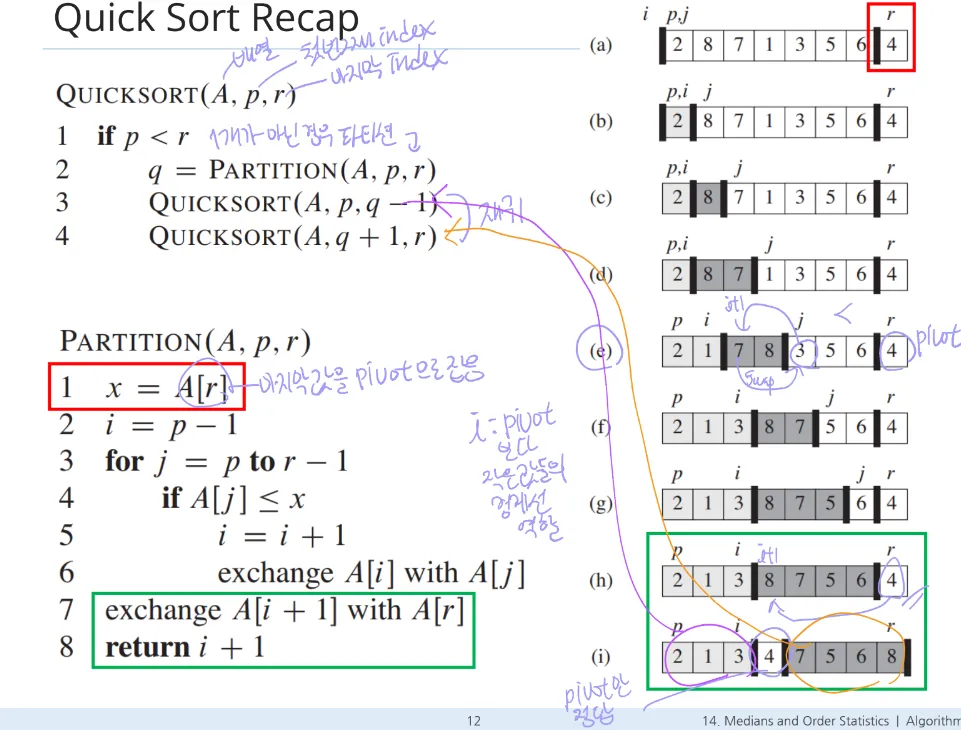
02. Quick Sort
- Quick Sort는 배열의 요소들을 피벗을 기준으로 나누고, 각 부분을 재귀적으로 정렬하는 분할 정복 기반 정렬 알고리즘
- 과정:
- 배열에서 하나의 피벗을 선택
- 피벗을 기준으로 작은 값들은 왼쪽, 큰 값들은 오른쪽으로 나누는 분할(partition) 작업 수행
- 각 부분을 다시 재귀적으로 정렬
- 최악의 경우(worst case): 피벗이 항상 가장 크거나 가장 작은 값을 선택하게 되면, 정렬이 한쪽으로 치우쳐 O(n^2)의 시간이 소요됨
03. Randomized Quick Sort
- 랜덤화된 퀵 정렬(Randomized Quick Sort)은 최악의 경우를 피하기 위해 피벗을 무작위로 선택하는 방법을 사용 -> 이로 인해 피벗이 비대칭적으로 선택되는 경우의 확률이 낮아져, 평균적인 시간 복잡도를 O(nlogn)로 유지할 수 있음
- 완전히 최악의 경우를 피할 수 있나: 완벽하게 방지할 수는 없지만 그래도 worst case를 피할 확률이 높아지는 것임

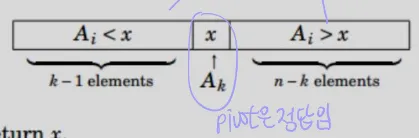
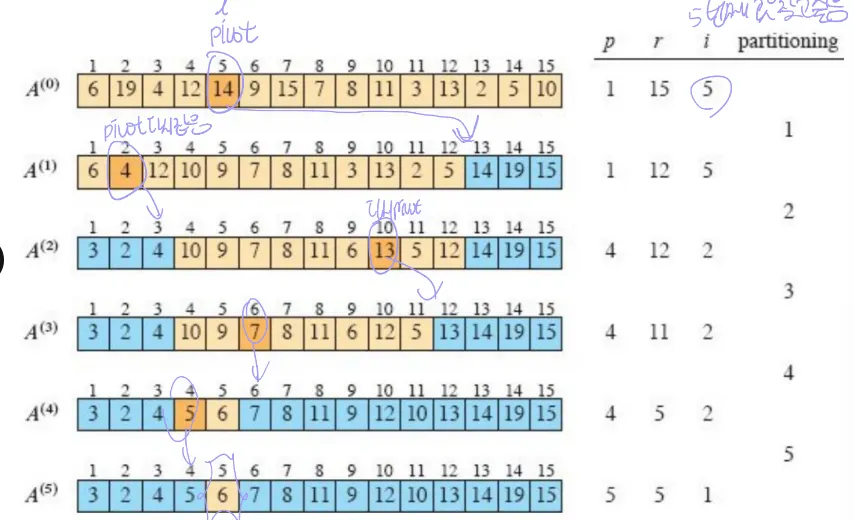
04. Quick Select - Randomized Select
- Quick sort를 수정하여 사용 → partition하는 과정은 동일, pivot은 정답값임
- 원래 기존 버전은 worst가 n^2, 평균이 n인데 랜덤화 시키면 최악 경우 확률을 낮춰서 평균 n임




'🌙CS > 알고리즘' 카테고리의 다른 글
| [Backtracking] 미로 탈출 (0) | 2024.11.22 |
|---|---|
| [DP] LCS (Longest Common Subsequence) (0) | 2024.11.21 |
| Sorting in Linear Time (0) | 2024.10.26 |
| Heap Sort (0) | 2024.10.26 |
| Matrix Multiplication (Strassen’s Algorithm) (0) | 2024.10.26 |
